ЗДОРОВЬЕ ТЕЛА И ДУШИ

Интересные головоломки  Задача третья

В этот раз для разминки приготовлена новая задача из серии: "Интересные головоломки". Эта задача отличается от предыдущих и является геометрической. На сей раз подумаем о благоустройстве  дач. Конечно, и решение здесь!

Профессор. Теперь рассмотрим задачу, связанную с геометрией. Пусть в дачном поселке слева от дороги находятся три дома, а справа  — три колодца с коллекторами (водопроводным, электрическим и газовым). Требуется каждый дом соединить с каждым коллектором, но так, чтобы траншеи с линиями соединений из соображений безопасности не пересекались. Как это сделать?

Простак. Придется повозиться с чертежами.    Похоже, соеди­нительные линии не могут быть пря­мыми, поскольку при первом рассмот­рении прямые линии пересекаются.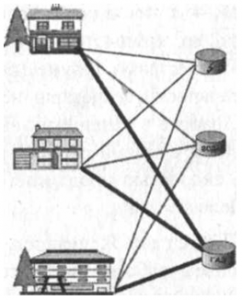 Если же линии сделать извилистыми, то для всех линий, кроме двух, задачу ре­шить легко, применяя обводки. Но вот развести эти оставшиеся две линии не получается. Мне кажется, что эту зада­чу вообще нельзя решить.

Профессор. Некоторые зада­чи могут не иметь решения, но в таких случаях это необходимо дока­зать. Иначе вы можете только утвер­ждать, что вам пока не удалось найти решения из-за недостатка времени, зна­ний, ума или еще чего-нибудь.

Зануда. Да, я слышал, что гра­фы (множество точек, соединен­ных линиями) могут иметь или не иметь так называемое свойство планарности. У планарного графа, расположенного в  одной  плоскости,  соединительные линии   не   пересекаются.   Планарные графы применяются при разработке пе­чатных плат для электронных устройств. Действительно, нельзя допустить, чтобы неизолированные проводники электрического тока пересекались. Так что надо доказать возможность построения соответствующего нашей задаче — обладающего свойством планарности. Или, наоборот, доказать, что такой граф не возможен. Однако для этого требуются специальные знания, которых у нас нет. Разумеется, я бы мог разыскать подходящий учебник, но там наверняка много комбинаторики, чего я не люблю. Как бы то ни было, данная задача мало похожа на головоломку. Для ее решения больше нужны конкретные знания, чем смекалка и здравый смысл, которых обычно вполне достаточно для разрешения головоломок.

Профессор. Прекрасно, что вы оба решили сначала создать математическую модель ситуации, описанной в условии задачи. Сам собой напрашивается подход: надо заменить дома точками одного сорта, а коллекторы — точками другого сорта. Тогда, как будто, задача сводится к поиску требуемых соединений разносортных точек. Первые эксперименты привели Простака к неудаче. Но, может, он просто провел мало эксперимен­тов? А может быть решения просто не существует, что, однако, нельзя дока­зать сколь угодно длительными неудачными экспериментами. Недостаток ваших специальных знаний из теории графов я компенсирую тем, что под­скажу: для принятой модели планарный граф не существует. Но что из этого следует?

Простак. Ваш вопрос, Профессор, по меньшей мере, странен. Вы же только что сами на него ответили: задача не имеет решения.

Зануда. Как-то не верится, что с виду незамысловатая инженерная задача, наверняка уже встречавшаяся проектировщикам дачных посел­ков, неразрешима. Что же получается, мы должны отказать заказчику в вы­полнении проекта?

Профессор. Не спешите с оконча­тельным ответом. Что мы установили? Только то, что задача неразрешима в рамках принятой модели. Интуиция подсказывает нам, что исходная практическая задача должна иметь решение — ведь разнородные коммуникации как-то разводят, причем даже в более сложных случаях. Например, часто требуется добавить еще телефонные и телевизионные кабели, а также выделенные линии связи с Интернетом, не говоря уже о канализации.

Простак. Я кажется, понял, в чем дело. Надо прокладывать линии на разных уровнях по глубине или высоте. Странно, что я раньше об этом не догадался.

Зануда. Но это уже не математическая задача.

Профессор. Уважаемый Простак сразу же решил задачу практиче­ски, но, надо признать, после некоторых околоматематических мытарств. А Вы, уважаемый Зануда, как будто потеряли интерес к задачке, едва почувствовав, что ее решение находится вне математики. Давайте еще раз зафиксируем то, что мы получили в попытках решить задачу с помощью математики. Мы приняли некоторую математическую модель и убедились, что в ее рамках задача неразрешима. А какова наша модель? Кроме условно­го изображения домов точками одного сорта, коллекторов — точками друго­го, а траншей между ними — линиями, мы еще неявно предположили, что результат решения должен располагаться в одной плоскости. Если вполне естественно допустить, что дома и коллекторы находятся в одной плоскости, то разве в условии задачи требовалось, чтобы траншеи проходили в этой же плоскости? Как и в случае первой задачи о числах, вы невнимательно отне­слись к формулировке условия. Если бы явно требовалась планарность графа соединений домов с коллекторами, то ваша модель была бы вполне подхо­дящей к данной практической задаче, и ее решение выглядело бы несколько необычно для обычных людей: решение не существует. В подобных случаях, как правило, заказчика просят как-то изменить условия задачи, чтобы она была, по крайней мере, разрешима. Теперь, я надеюсь, вы согласитесь, что рассмотренная задача все же относится к головоломкам, поскольку требует для своего решения только внимания и немного смекалки.

Эта интересная головоломка подготовлена по материалам книги  Вадима Дунаева «Занимательная математика. Множества и отношения». До новых встреч!

Еще одна головоломка [...]