ЗДОРОВЬЕ ТЕЛА И ДУШИ

Очередная интересная алгоритмическая задача! На сей раз нам предстоит поиск фальшивой монеты. Приступим.

Профессор. Вот новая задача. Пусть среди восьми с виду одинаковых монет нахо­дится одна фальшивая,  которая легче настоящих.  Как выявить фальшивую монету, используя рычажные весы не более двух раз?

Простак. Очевидно, что взвешивая пару монет (на каждой чаше ве­сов по одной монете), мы можем ограничиться всего лишь одним взвешиванием, но только если нам повезет: фальшивая монета окажется в выбранной для взвешивания паре. В худшем случае нам потребуется четы­ре взвешивания. Я где-то слышал о решении похожей задачи, которая, ка­жется, называется "поиск льва в пустыне". Там вся пустыня разбивалась на две одинаковых области и по рыку льва определялось, в какой из областей он находится. Эта область, откуда разносился рык, делилась пополам и снова определялась подобласть, где обретается лев. Данная процедура продолжа­лась до тех пор, пока область разбиения не оказывалась настолько малой, чтобы мы могли с уверенностью сказать: "Вот лев." Не кажется ли вам, что между поисками льва и фальшивой монетой есть аналогия?

3 а н у д а. Если воспользоваться аналогией Простака, то требуется разбить множество из восьми монет на два подмножества из четырех монет и сравнить их веса. Выбрать самое легкое подмножество (именно там находится фальшивая монета) и разбить его пополам, чтобы затем сравнить эти половины на весах. Аналогичным образом следует поступать до тех пор, пока на чашах весов не окажется по одной монете. На этом последнем этапе взвешивание и выявит фальшивую, более легкую, монету. Нетрудно подсчи­тать, что данная стратегия потребует трех взвешиваний, а не двух, как указа­но в задаче. Так что либо "поиск льва в пустыне" — плохой метод, либо по­ставленная задача неразрешима.

Простак. Я вспомнил о методе поиска льва потому, что он был са­мым быстрым. Поэтому я склонен считать, что либо двумя взвешива­ниями нельзя определить одну фальшивую монету из восьми, либо аналогия между задачами о льве и взвешиваниях недостаточно полна, чтобы лучший метод для первой задачи оказался лучшим и для второй.

Профессор. Я вижу, что рассмотрение предыдущих задач не про­шло для вас даром.

Зануда. Я не могу отказаться от использования, хотя бы частичного, аналогии с задачей о льве. Может быть, попробовать делить множест­во монет не на два, а на большее количество подмножеств? Что будет, если разбить множество монет на три подмножества?

Простак. Конечно, можно попробовать. Но сравнивать по весу мы можем только два подмножества. Более того, сравнивать надо только подмножества, содержащие одинаковое количество монет. При этом сравни­ваемые множества могут оказаться и равными по весу, в отличие от случая деления пополам. Наконец, разбить множество из восьми монет на три под­множества можно несколькими способами. Какой из них выбрать?

Зануда. Способов разбиения восьми монет на три подмножества не так уж и много. Не перебирая все возможные варианты, следует вы­брать тот из них, при котором количества монет в подмножествах наиболее близки друг к другу. Очевидно, что первые два подмножества должны со­держать по три монеты, а последнее — оставшиеся две (3 + 3 + 2 = 8).

Простак. Хорошо, но что взвешивать на первом этапе? Фальшивая монета может оказаться в любом из трех множеств, а результат взве­шивания может ничего не дать: сравниваемые множества могут оказаться одинаковыми по весу.

Зануда. Если сравниваемые множества одинаковы по весу, то это означает, что ни в одном из них нет фальшивой монеты и, следовательно, она находится в третьем множестве. А разве это не положи­тельный результат, не информация для планирования последующих действий?

Простак. Действительно, я был опрометчив в своих оценках. Тем не менее, с чего начать? Следует ли сначала сравнить на весах две монеты из третьего множества, или же сравнить первые два множества, со­держащие по три монеты?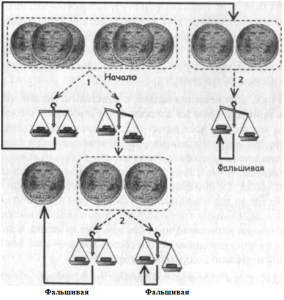

Зануда. Для меня очевидно, что начать надо с двух множеств, со­держащих по три монеты. Впрочем, ты можешь поступить иначе, что­бы убедиться в возможности варианта, когда двух взвешиваний тебе не хва­тит. Итак, сравним два множества, по три монеты в каждом. Тогда возможны два варианта:

1. Оба множества весят одинаково, т. е. в них нет фальшивой монеты. В дан­ном случае переходим к третьему множеству из двух монет, сравнение ко­торых на весах и укажет фальшивую. В итоге мы нашли фальшивую мо­нету посредством двух взвешиваний.
2. Трехмонетные множества различаются по весу. Тогда выбираем наиболее легкое из них и взвешиваем любые две монеты. Это (второе по счету) взвешивание сразу укажет фальшивую монету, независимо от того, равны ли по весу сравниваемые монеты. Действительно, если сравниваемые мо­неты имеют разный вес, то самая легкая из них— фальшивая, а если ни одна из них не перевешивает другую, то фальшивой является третья моне­та, которую мы не клали на чашу весов. Таким образом, и в этом варианте мы обошлись всего двумя взвешиваниями.

   Итак, поиск фальшивой монеты состоялся. Впереди - другая интересная алгоритмическая задача! Еще одна алгоритмическая задача [...] До новых встреч!

   Статья подготовлена по материалам книги Вадима Дунаева «Занимательная математика. Множества и отношения»